Estereorradián

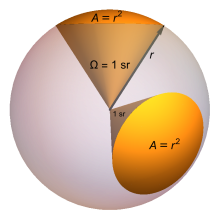
El estereorradián (símbolo: sr) es la unidad derivada del SI que mide ángulos sólidos.​ Es el equivalente tridimensional del radián.​

El estereorradián, como el radián, es una unidad adimensional,​​​ el cociente del área subtendida y el cuadrado de su distancia al centro. Tanto el numerador como el denominador de esta relación tienen una dimensión de longitud al cuadrado (es decir, L²/L² = 1, adimensional). Sin embargo, es útil distinguir entre cantidades adimensionales de diferente naturaleza, por lo que el símbolo "sr" se usa para indicar un ángulo sólido. Por ejemplo, la intensidad radiante se puede medir en vatios por estereorradián (W⋅sr⁻¹). El estereorradián era anteriormente una unidad suplementaria del SI, pero esta categoría fue abolida en 1995 y el estereorradián ahora se considera una unidad derivada del SI.​

El estereorradián es una unidad importante para medir la distribución espacial de diversos fenómenos, desde la luz y la radiación hasta el sonido y los campos visuales. Sus aplicaciones abarcan diversos campos científicos como la astronomía, la radiometría, la geodesia, los gráficos por computadora y la acústica, permitiendo una modelización y cuantificación precisa del espacio tridimensional. Comprender y utilizar los estereorradianes permite realizar mediciones más precisas y optimizaciones tanto en tecnología como en la investigación científica.

El estereorradián se define haciendo referencia a una esfera de radio ${\displaystyle r=1m}$. Si el área de una porción de esta esfera es ${\displaystyle r^{2}}$, un estereorradián es el ángulo sólido comprendido entre esta porción y el centro de la esfera.

El ángulo sólido en estereorradianes es

${\displaystyle \Omega ={\frac {S}{r^{2}}}\,}$,

donde ${\displaystyle S\,}$ es la superficie cubierta por el objeto en una esfera imaginaria de radio ${\displaystyle r\,}$, cuyo centro coincide con el vértice del ángulo.

Por tanto, un estereorradián es el ángulo que cubre una superficie ${\displaystyle r^{2}\,}$ a una distancia ${\displaystyle r\,}$ del vértice,

${\displaystyle \ 1sr={\frac {r^{2}}{r^{2}}}\,}$.

Analogía con el radián

En dos dimensiones, el ángulo en radianes, está relacionado con la longitud de arco, y es:

${\displaystyle \theta ={\frac {s}{r}}\,}$,

siendo ${\displaystyle s}$ la longitud de arco, y ${\displaystyle r}$ el radio del círculo.

Si el área ${\displaystyle A\,}$ es igual a ${\displaystyle r^{2}\,}$ y está dada por el área de un casquete esférico (${\displaystyle A=2\pi rh\,}$), entonces se cumple que

${\displaystyle {\frac {h}{r}}={\frac {1}{2\pi }}}$.

Por lo tanto, el ángulo sólido descrito por el cono que corresponde al ángulo (plano, vea la figura) es igual a:

${\displaystyle \Omega =2\pi \left(1-\cos \theta \right)\,\mathrm {sr} }$.

Si A = r², corresponde al área de un casquete esférico (A = 2π r h) (donde h es la "altura" del casquete) y vale la relación h/r = 1/2π. Por lo tanto, en este caso, un estereorradián corresponde al ángulo plano (o sea en radián) de la sección transversal de un cono simple que comprende el ángulo plano 2θ, con θ correspondiente a :

${\displaystyle {\begin{aligned}\theta &=\arccos \left({\frac {r-h}{r}}\right)\\&=\arccos \left(1-{\frac {h}{r}}\right)\\&=\arccos \left(1-{\frac {1}{2\pi }}\right)\approx 0.572\,{\text{ rad,}}{\text{ o }}32.77^{\circ }.\end{aligned}}}$

Este ángulo corresponde al ángulo de apertura plano de 2θ ≈ 1.144 rad o 65.54°.

Un estereorradián también es igual al área esférica de un polígono que tiene un exceso de ángulo de 1 radián, para 1/4π de una esfera completa, o de 2
≈ 3282.80635 grados cuadrados.

El ángulo sólido de un cono suya sección transversal define un ángulo 2θ es:

${\displaystyle \Omega =2\pi \left(1-\cos \theta \right)\,{\text{sr}}=4\pi \sin ^{2}(\theta /2)\,{\text{sr}}}$.

Respecto a las unidades utilizadas en el Sistema Internacional de Unidades, miliestereorradianes (msr) y microestereoradianes (μsr) se utilizan en forma ocasional para describir los haces de luz y de partículas.​​ Otros múltiplos rara vez se utilizan.

El estereorradián se utiliza en radiometría​ y fotometría.​​ La intensidad radiante se expresa en vatios por estereorradián​ y la radiancia, en vatios por metro cuadrado estereorradián.​

• La mirada de un ojo humano abarca aproximadamente 2π sr.​
• Un cono circular, con medio ángulo en el vértice θ, corta en el espacio un ángulo sólido de 2π (1 - cosθ) estereorradianes. Un ejemplo concreto ilustra la relación entre un ángulo sólido (en el espacio) y el ángulo de vértice correspondiente (ángulo habitual en un plano): Si giramos un ángulo plano (2θ) de 1,144 radianes (65,54°) alrededor de su bisectriz, genera un cono que define un ángulo sólido de 1 estereorradián.

El lumen es la unidad de flujo luminoso correspondiente al flujo emitido por una fuente con una intensidad luminosa de 1 candela contenida en un ángulo sólido de 1 estereorradián.

Expresiones que contienen el estereorradián:

${\displaystyle \mathrm {1\,lm=1\,cd\cdot 1\,sr} }$

y

${\displaystyle \mathrm {1\,lx={\frac {1\,cd\cdot 1\,sr}{1\,m^{2}}}} }$

con:

• lm: lumen que es la unidad de flujo luminoso;
• sr: estereorradián que es la unidad de ángulo sólido;
• cd: candela que es la unidad de intensidad luminosa;
• lx: lux que es la unidad de iluminancia de la luz.

Astronomía y Astrofísica

En astronomía, el estereorradián se usa ampliamente para cuantificar el tamaño aparente de los objetos celestes. Por ejemplo, el diámetro angular de la Luna o una estrella visto desde la Tierra puede medirse en estereorradianes. Dado que la Tierra suele ser utilizada como punto de referencia, comprender el estereorradián permite a los astrónomos calcular el área aparente del cielo ocupada por los objetos astronómicos y la intensidad de la radiación emitida desde o que pasa a través de esos objetos.

Radiometría y Fotometría

En el campo de la radiometría, que se ocupa de la medición de la radiación óptica (incluyendo la luz visible), los estereorradianes son esenciales para determinar la radiancia o el flujo luminoso de una fuente.​ La cantidad de energía radiante emitida en una dirección particular a menudo se mide en términos de vatios por estereorradián. Esto ayuda a determinar cuánta energía se emite por unidad de ángulo sólido, lo cual es importante para caracterizar las propiedades direccionales de fuentes de luz, como láseres o bombillas.​​

Geodesia y Cartografía

En geodesia, que se ocupa de la medición y representación de la superficie terrestre, el estereorradián se usa para calcular áreas sobre la superficie esférica de la Tierra. Por ejemplo, cuando se mide el tamaño de una región sobre la superficie de la Tierra, el área puede calcularse en estereorradianes. Este uso es fundamental en la navegación y la elaboración de mapas, especialmente cuando se trabajan con proyecciones que modelan la curvatura de la Tierra.​

Gráficos por Computadora y Visión

En gráficos por computadora y visión, los estereorradianes se utilizan para modelar el campo de visión de cámaras y cámaras virtuales. El campo de visión (FoV, por sus siglas en inglés) en gráficos por computadora 3D puede expresarse en términos de estereorradianes para cuantificar cuánto de la escena virtual es visible a través de la lente de la cámara. En sistemas de realidad virtual (VR) o aumentada (AR), este concepto es crucial para simular cómo los usuarios perciben los entornos 3D.

Acústica y Medición del Sonido

Los estereorradianes también tienen aplicación en acústica, donde ayudan a medir la intensidad y distribución del sonido en el espacio tridimensional. Las fuentes sonoras, como altavoces o instrumentos, pueden caracterizarse en términos del ángulo sólido que cubren, lo que permite una modelización más precisa de la distribución del sonido, especialmente en acústica arquitectónica e ingeniería de audio.​

• I. Mills, Tomislav Cvitas, Klaus Homann, Nikola Kallay, IUPAC (June 1993). Quantities, Units and Symbols in Physical Chemistry (2nd edición). Blackwell Science Inc. p. 72. 
• Hall, Arthur Graham; Frink, Fred Goodrich (January 1909). «Chapter VII. The General Angle Signs and Limitations in Value. Exercise XV.». Escrito en Ann Arbor, Michigan, USA. Trigonometry. Part I: Plane Trigonometry. New York, USA: Henry Holt and Company / Norwood Press / J. S. Cushing Co. - Berwick & Smith Co., Norwood, Massachusetts, USA. p. 73. Consultado el 12 de agosto de 2017. 
• International Bureau of Weights and Measures (20 de mayo de 2019), The International System of Units (SI) (9th edición), ISBN 978-92-822-2272-0, archivado desde el original el 8 de mayo de 2021 .
• Brinsmade, J. B. (December 1936). «Plane and Solid Angles. Their Pedagogic Value When Introduced Explicitly». American Journal of Physics 4 (4): 175-179. Bibcode:1936AmJPh...4..175B. doi:10.1119/1.1999110. 
• Romain, Jacques E. (July 1962). «Angle as a fourth fundamental quantity». Journal of Research of the National Bureau of Standards, Section B. 66B (3): 97. doi:10.6028/jres.066B.012. 
• Eder, W E (January 1982). «A Viewpoint on the Quantity "Plane Angle"». Metrologia 18 (1): 1-12. Bibcode:1982Metro..18....1E. doi:10.1088/0026-1394/18/1/002. 

• Ley de Lambert